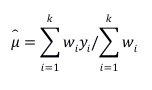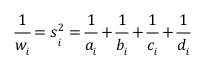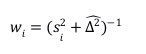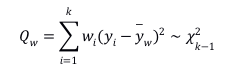Meta分析的历史最早可以追溯到1925年Fisher先生的合并P值方法(Fisher's combined probability test)。也就是说,Meta分析其实是一个非常朴素的想法,即:当我们针对同一个假设做了多个独立的研究时,自然想得到一个最终的结果作为判断依据,而我们希望这个结果能比其中任意一个单独的结果更接近真值。
那么,所面临的第一个问题,也是最本质的问题,即是:为什么针对同一个假设的不同研究结果会有所不同?或者更进一步,我们针对同一个假设做了多个理想的RCT研究(假设不存在依从性问题和失访问题),而众所周知,RCT的结果是不存在偏倚的,所以结果理应都是真实无偏的,那么为什么结果仍然会有区别?我相信大家的第一反应都是:当然是因为随机误差的存在。因为我们每一个RCT的研究样本均假设为从某个目标总体随机抽样而来,也就是说如果研究使用无偏一致的估计量,那么得到的效应量与真值之间的差别则仅仅是因为随机所致,而随着样本量的增加,效应量会一致收敛于真值。知道问题的答案,下一步就简单了,不同RCT因为样本量的区别,所以估计的精确度不同,精确度高的研究的效应量理应有更高的价值。因此,一个很自然的Meta分析步骤即是给每一个RCT的效应量赋予一个权重,精确度高的效应量权重大,精确度低的权重小。而通常情况下,精确度是通过方差来衡量,方差大的精确度低所以权重小,因此,我们只需要取方差的倒数作为效应量的权重,算一个加权平均效应量即可:
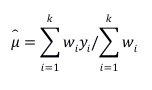
当效应量取OR时,这个方法退化为Mantel-Haenszel estimator,此时权重为:
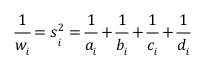
当权重仅取“倒方差”时,模型称为固定效应模型,意为仅取研究内方差作为权重。而当权重同时考虑研究内方差和研究间方差时,则变为随机效应模型,等同于随机效应方差分析模型,即:
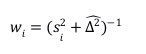
而从随机效应模型中,即可以引出Meta分析的异质性检验,也就是检验随机效应中的研究间方差是否显著,当效应量取OR时,此方法退化为Woolf Method,即:
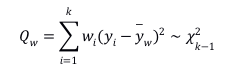
到此为止,问题好像都解决了,我们依据不同RCT样本量的区别所导致的精确度差异进行加权,最后合并的加权效应量完美的解决了单个RCT样本量小的问题,并且通过合并增加样本量,来使效应量一致、逼近真值。我们即得到了相比于任何一个单独的RCT的效应量更准确的、更真实的合并效应量。细心的同学可能会发现,上述Meta分析少了一个步骤,那就是亚组分析或Meta回归。不知道有没有人质疑过,为什么Meta分析必须做亚组分析?不做可以吗?如果按照前面说的那样,Meta分析的问题应该都解决了,那么问题出在哪?
回过头来再看我们第一个提出的问题:为什么针对同一个假设的不同研究结果会有所不同?刚才的答案是因为随机误差的存在,而现在我们需要再加一个因素:因为效应修饰的存在。效应修饰是什么?每一个RCT的样本特征不同,即基线协变量的联合分布不同,使得不同RCT出现相对应于其基线分布特点的效应量。比如,简单的说就是,第一个RCT中纳入患者的年龄分布是20~30岁,而第二个RCT中纳入患者的年龄是40~50岁。那么不同年龄组的患者所得到的效应量理应不同。很多人可能会把效应修饰和混杂因素混淆,事实上,这是完全不同的两个东西。当我们的情景中符合条件可交换性时,也就是例如我们在进行一个分层随机试验,除去分层变量的影响,在每一层中的干预组和对照组之间的患者特征是平衡的,也就是在每一层中进行一个完全随机试验,即层内效应量是没有偏倚的。这种情况下,不同层间出现的效应量差别被称为效应修饰现象。当这个分层变量同时可以被看作是另一个干预时,这个现象被称为交互效应。明白这点之后,我们就可以理解,其实对于不同的RCT本身,并不存在混杂因素的影响,但是存在效应修饰的影响。在Meta分析的Mantel-Haenszel方法中,事实上,当我们估计加权效应量时,一个很重要的假设即是:不同RCT之间不存在异质性。这话啥意思,啥叫异质性?依据Cochrane给出的定义,将异质性分为三部分:临床异质性、方法学异质性、统计学异质性。首先方法学异质性是指由于RCT本身的质量差异所导致的差异。然后是临床异质性,定义为由于纳入研究的患者特征不同所导致的差异,也就是我们前面所讲的效应修饰问题。最后的统计学异质性就不难理解了,RCT之间的数据本身的差异,可以同时包括上述其他异质性。但是需要注意,不同RCT之间本身也存在随机误差,所以,当我们在说统计学异质性时,必然也包括随机误差的存在。那么,在Meta中,不存在异质性这个假设本身并没有说清楚,其实正确的说法应该是:不存在随机误差以外的异质性。当忽略方法学异质性时,这个说法变为:不存在效应修饰。既然,明确了假设的定义以后,那么剩下的问题就是判断是否存在效应修饰。如何判断?我想大多数同学的第一反应是:异质性检验。如前所述,异质性检验即是通过计算研究间方差的统计量,依据其零假设下服从卡方分布的原理,计算P值,如果P值小于某个门槛(例如0.05或0.1),我们认为存在异质性,反之,不存在异质性。在这里我不想说P值本身的问题,即使假设这个异质性检验在统计意义上完美执行,它依然是有问题的。
问题在于,异质性检验是依据数据本身进行,也就是它检验的是上述统计学异质性。而统计学异质性除了效应修饰作用以外,还有随机误差。事实上,就算我们检验出存在统计学异质性,也无法分辨具体是效应修饰的作用还是随机误差的作用。比如,其中效应修饰的方向与随机误差方向相同,两者叠加可能互相更远离彼此,即存在统计学异质性。或者两者方向相反,互相抵消,即不存在统计学异质性。所以,异质性检验是无法区分效应修饰和随机误差的。那么,现在回到上面的另一个问题:亚组分析。此时,我们就可以很明确的看出亚组分析的一个主要作用,即:分析是否存在效应修饰。通过对合并后的效应量,基于不同的患者特征进行分层分析,看看不同层间效应量是否存在差异,如果存在,说明这个分层特征即是一个效应修饰因子,也就是假设不成立。通过对许多不同的基线特征进行分层,分别看每一个特征是否存在效应修饰作用。亚组分析似乎是一个不错的方法,但是好像也有问题,因为每次只分析一个基线特征,也就是这个分析策略包含着另一个假设,即:当我们分析其中某个特征时,默认其他特征不存在效应修饰。从这个角度看,这不是悖论吗?因为那么多特征中总有一个特征在亚组分析时,是没有显著差异的,如果我们想让这个结论本身可靠,必须假设其他特征没有效应修饰。那么我们还有必要分析其他特征吗?如果其他特征分析出显著差异时,上一个结论还可靠吗?那么,如何解决这个问题,一个自然的想法便是同时分析所有特征。这个方法被称为:多变量Meta回归。如果说亚组分析是非参方法,那么Meta回归就可以称为参数模型方法。在前面介绍的效应量合并方法中,M-H法就是非参方法,事实上也可以用广义线性模型,二者是一个道理。Meta分析的所有模型方法均可以用多水平模型来解释,即直接在level-2水平中建模。那么自然也可以再多纳入几个特征变量进行Meta回归分析。多变量Meta回归看似挺好的解决了亚组分析的假设问题,但是又引出了另外的问题,即:无论是亚组分析或Meta回归,我们只能将每一个RCT中的某个特征进行均值处理,也就是进行分析时,其实分析时只用到了基线特征的均值,甚至方差信息都没用到,例如平均年龄25岁标准差10岁,和平均年龄25岁标准差25岁,能一样吗?而我们的分析策略就是将两者看成一样的。更进一步,如果原分布不对称呢?均值能很好的反应总体趋势吗?所以,问题就是:我们无法考虑基线特征的分布。这个问题暂时放在一边,回到开始那个更重要、更本质的问题:如果检验出确实存在效应修饰作用,也就是说“不存在随机误差以外的异质性”这个假设不成立时,会怎么样?当提到存在异质性时,我相信大部分人都会选择随机效应模型来合并效应量,的确,从统计学角度来看,存在异质性也就意味着存在研究间方差。那么随机效应模型怎么处理的?简单的讲,其实就是将这部分估计出的研究间方差重加权至效应量中,也就是当我们使用随机效应时,意味着我们计算了两次加权效应量,第一次仅有研究内方差,第二次同时存在研究内和研究间方差。这样估计确实有一定好处,通过改变权重(本质上是使权重更平均化),来更保守的计算合并效应量。然而,很明显,上述过程同样是一个纯统计学的过程,所以必然带有统计学假设,即:研究间方差服从N(0, σ2)。这个假设合理吗?好像有一些道理。那么解决我们的问题了吗?回来再看我们的问题,如果存在效应修饰作用怎么办。随机效应模型给出的答案是,管他存在什么作用,全部归为一个呈正态分布的随机变量,简单粗暴。无论从哪个角度看,这个方法依然是一个权宜之计,没有从根本上解决这个问题。为什么这么说,因为上述随机效应模型的估计过程和固定效应一样,在合并效应量估计时,仅仅使用到RCT中的均值和方差(或标准误),没有更多的信息了。而事实上,RCT中的标准误仅仅代表这个均值的精确度,不能代表基线特征的效应修饰作用。所以,现在看似一大堆奇奇怪怪的Meta分析方法(包括贝叶斯方法),本质上并没有突破上述问题,或者说与1959年的M-H方法相比并没有实质性的进步。那么更为关键的问题在哪?随机效应模型尽管粗糙,但是合并效应量依然比某一个单独的RCT效应量更精确、更接近真值不是吗?并不一定。如前所述,无论我们使用异质性检验、亚组分析、Meta回归,均无法很好的分辨出是否真的存在效应修饰作用,甚至总是和随机误差混淆,因为两者的作用可能叠加或者抵消。事实上,如果使用OR作为效应量会变得更加不可预料,因为OR的non-collapsibility性质,使得不同层内的条件OR值不能通过加权平均的方法得到边际OR值(Greenland 1987)(原理见Jensen's inequality)。所以最终我们估计出的合并效应量是很难解释的,因为它并不是整个Meta分析纳入人群的目标总体中的因果效应估计,而是某种混合的合并效应。只有当不同RCT之间不存在效应修饰时,这个合并效应才会接近目标总体的因果效应,此时才有可解释的临床意义。然而,矛盾在于,我们无法判断是否存在效应修饰。如前所述,Meta分析的问题在于,只有不存在效应修饰时,合并效应量的解释才有临床意义,而矛盾之处在于,我们无法判断是否存在效应修饰。也就是,最终得到的合并效应量仅仅是某种混合效应,不一定具有因果解释。而这相比于原RCT解释力反而下降了,因为每一个RCT均有非常明确的因果效应解释,即:RCT纳入人群的目标总体的因果效应无偏估计。当我们对目标总体进行特征化后,即能很好的外推我们的结论(当然也不一定容易)。
在过去10年中,Meta分析研究飞速的增长,甚至连网状Meta分析研究也在近几年飞速增长。繁荣的背后即是泡沫。我想有相当数量的Meta分析的结论很有可能是错误的,并且有可能误导临床实践。当然网状Meta分析的结论就更玄了,现在连异质性的问题都没有解决,更不用说传递性了。所以,当我们看待Meta分析研究的结论时,应该小心、谨慎,更不要想当然的觉得Meta分析的证据等级一定高于单个RCT,无论任何证据都要进行质量评价,只有高质量的证据才有更高的效力,无论它是否是Meta分析。如前所述,Meta分析固有的一个缺陷,是最终的合并效应量并不能很好的被解释,只能是某种混合效应。这是一个很糟糕的情况,因为现在越来越多的RCT研究,如果不能做Meta分析,那么有时候会面临决策困难等问题,所以我们迫切需要解决的办法。在此之前,先说一下目前的现有一些其他讨论,比如18年BMJ上的一篇综述(Kent 2018),简单总结了一下异质性问题,提出大多数Meta分析研究中的亚组分析并不具备应有的统计学效力,所以无法很好的检验效应修饰。并且提出使用一些预测模型(包括lasso回归或岭回归一类的正则化回归方法)来处理异质性治疗效应。首先,我个人认为这篇文章并没有抓住实质问题,亚组分析的问题并不是具不具备统计学效力的问题,我们甚至可以假设它能完美检测出统计学差异,然后呢?能分清这个差异是效应修饰还是随机误差吗?说到底,效应修饰问题是一个识别问题,而随机误差是一个估计问题,两者根本不在一个层面上。两个维度的东西混杂在一起,而我们只能观测到最终的结果,怎么可能分辨出两者各自的效应。后面的预测模型也一样,可以一定程度上缓解这个问题,但是同样没有从根本上解决。那么我们应该怎么办?什么才叫从本质层面去解决?我们必须对待效应修饰呈不可知论,即在最初的合并分析中,必须假设我们对它一无所知,它可能有,可能没有,但是在我们的估计中必须不能体现出来,因为我们施加的模型假设很可能是错误的。所以,我们需要更多的信息,仅凭每个RCT的效应量和标准误当然是不够的,在这里需要引入IPD数据。其实很多年前就已经有了IPD-Meta分析,也就是个体病例数据(Individual patient data, IPD)Meta分析。我要说的是这个吗?明显不可能,如果这个问题早就解决就无需再说了。IPD-Meta分析其实本质上和普通Meta分析没有实质的区别,只不过更精准了一点。尽管用到的信息是每个RCT的全部个体数据,但是数据分析时,依然局限在使用每个个体的结局指标测量值上面,并没有更多的信息,而事实上每个RCT的效应量都是个体数据的无偏一致估计,所以本身一定程度上就可以代表个体数据分布。所以,很自然的想法便是,进一步使用所有个体的基线特征数据,也就是把它当成一个队列研究,其中包含全部结局数据和基线数据。因此,我们可以使用基线特征的经验分布对不同RCT(level-2水平)进行逆概率加权,同时在个体层面(level-1水平)中也使用逆概率加权,后者逆概率加权的识别条件即是当对不同RCT和不同基线特征进行分层时,干预组和对照组之间满足条件可交换性。当然,这只是识别过程,还需要进一步对其进行估计,这里就不展开说了。总之,如果我们想通过Meta分析的方法得到一个有明确解释的效应量,或目标总体的因果效应量,目前唯一的方法则是通过包含基线特征的IPD数据进行估计,尽管过程可能相对复杂,但是却是我们非常希望得到的效应量,也是具有明确因果解释的效应量。然后,在这个因果效应量上再进行亚组分析,那么此时得到的即是真实的效应修饰作用,具有直接临床决策的应用价值。
作者:石清阳