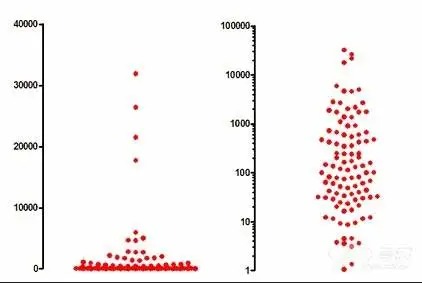
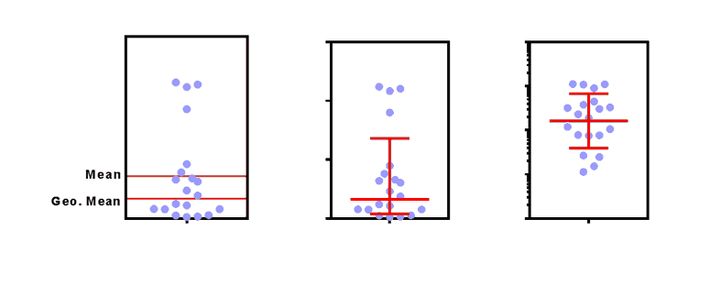
在对数轴上绘图时,如上图右侧所示,分布是对称分布; 如果你不知道对数正态分布,则可试图将上面示例中最高的四个值作为异常值进行删除,因为其看起来不属于总体分布。如果通过异常值检测算法(假设从高斯分布中抽样)来运行这些值,则可识别出异常值(上述示例中最高的四个值); 如果你尝试使用t检验或方差分析比较平均值,可能会发现P值很高,置信区间很宽。T检验和方差分析假设这些值是从高斯分布中抽样。如果你尝试使用这些方法来比较从对数正态分布中抽样的数据集的平均值,就会失去统计检验力; 对数正态分布中所有值的对数均为高斯分布。 如何处理对数正态分布? 如果数据是从 对数正态分布中抽样,则几何均值可能是表示分布中心的最佳方式。 注释:1.Kirkwood,TBL(1979)。"几何均值和离差度量”。《生物统计学》35:908–9 相关推荐: 「视频教程」GraphPad Prism 8 软件操作教程 中文字幕 「视频教程」手把手教你用GraphPad Prism做符合SCI投稿的标准图 GraphPad Prism 7 for Win / Mac 完美破解版 统计绘图软件 附安装教程 GraphPad Prism 8.4.3 for Win/Mac 最新完美激活中英文版医学绘图软件+安装教程 GraphPad Prism 9 for Win/Mac 完美学习版+安装教程