剂量反应案例研究:四参数 Logistic 模型
摘要:本篇案例分析,将利用 GraphPad Prism 8 中常见的「四参数 Logistic 回归模型」,分析来自某项剂量反应试验的数据。该试验目标是预估在有无增强剂(booster)的条件下,跳蚤治疗的 EC50 值。其试验结果是 500 只跳蚤中被杀死的跳蚤数量。
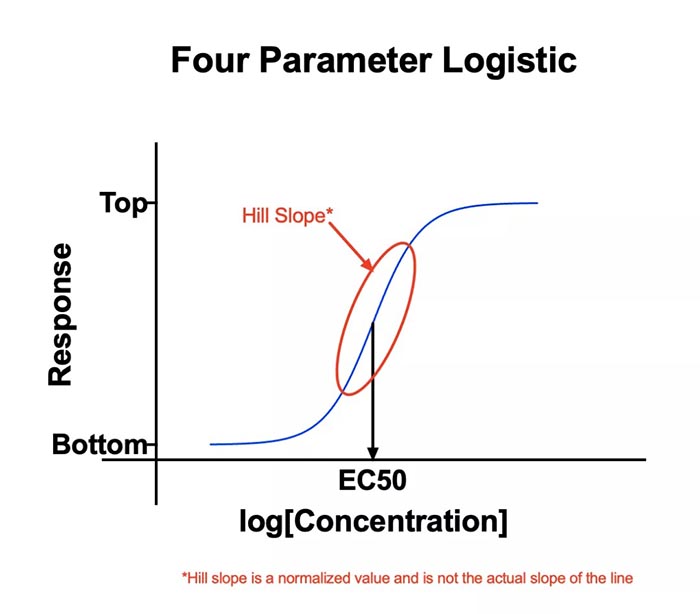
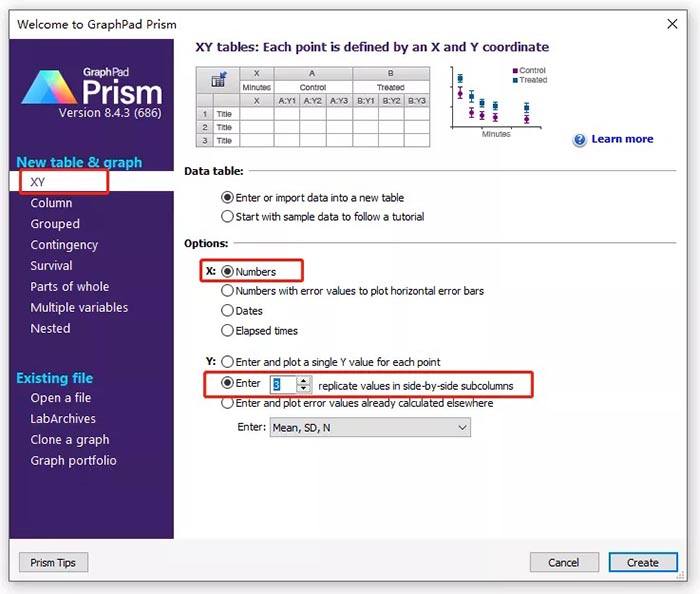
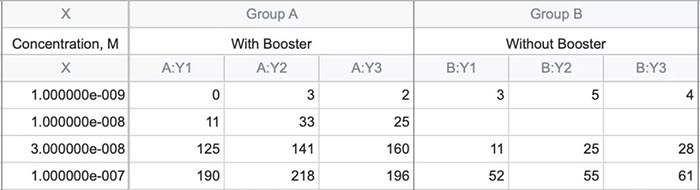
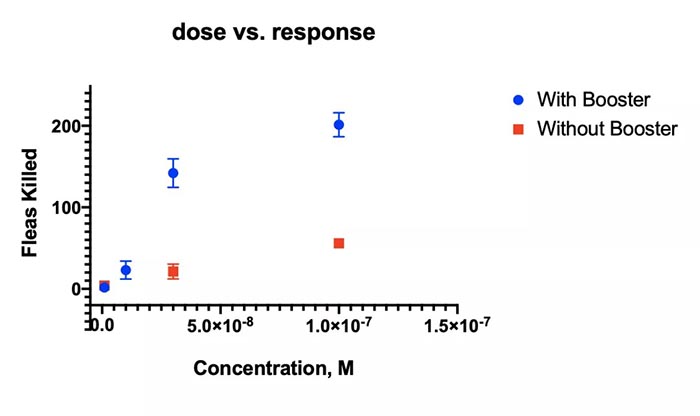
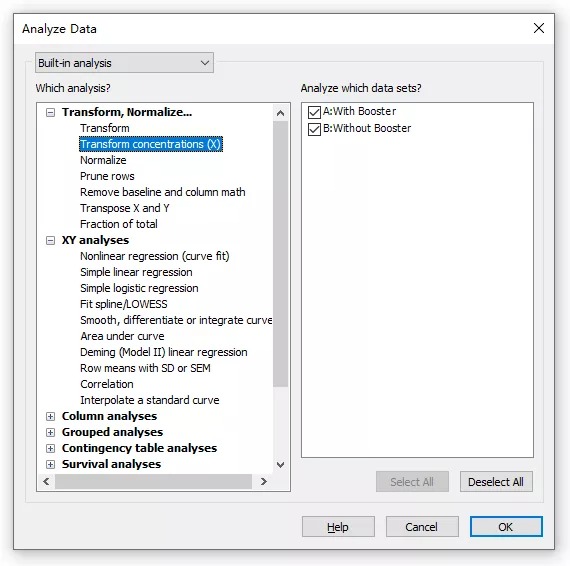
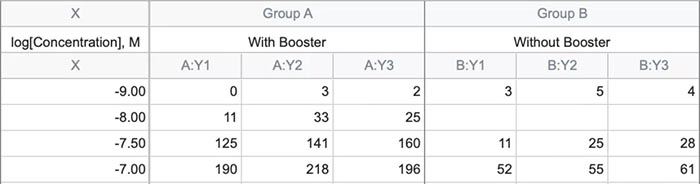
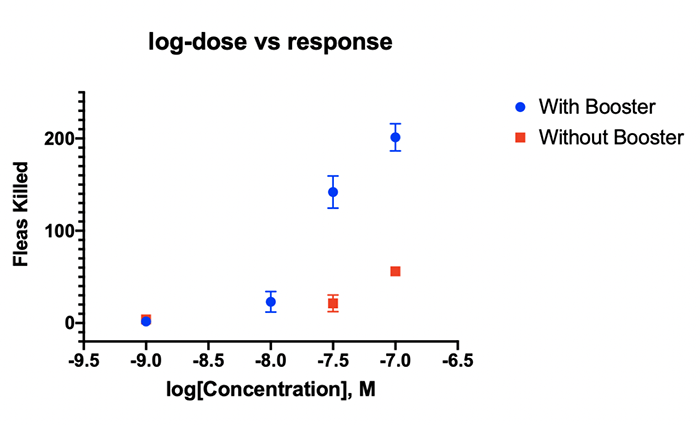
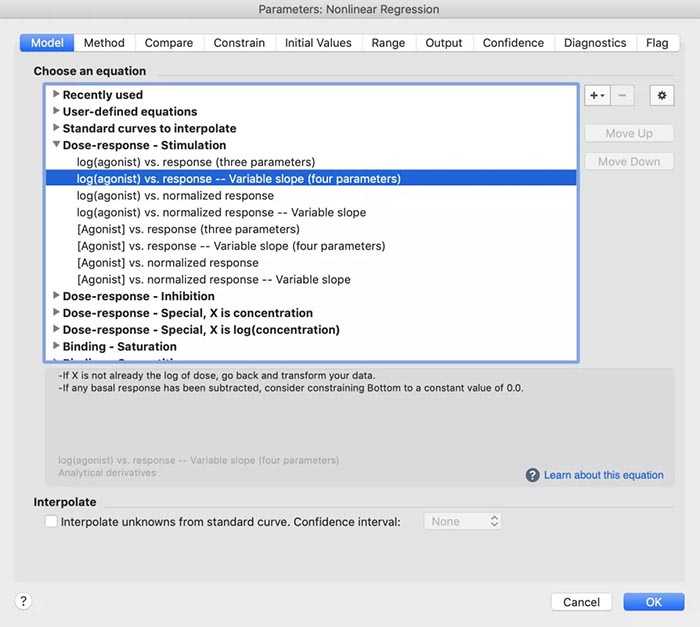
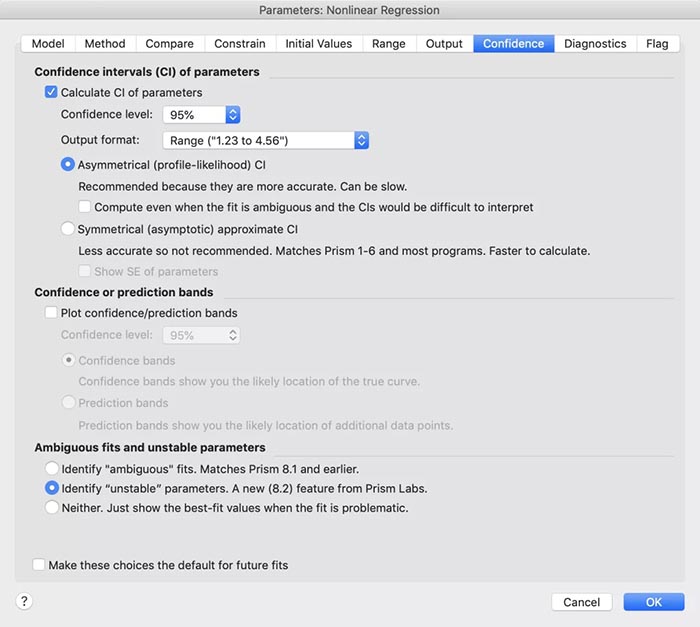
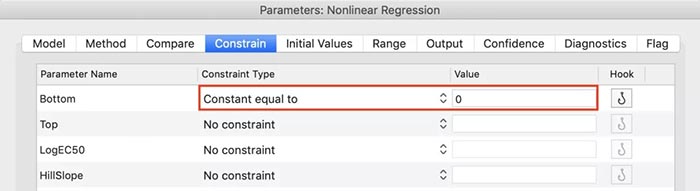
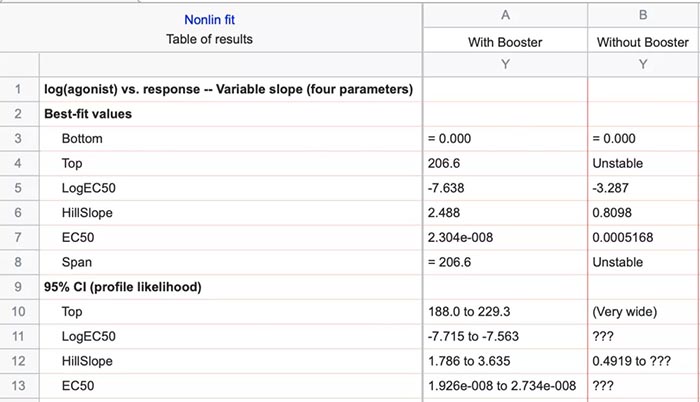
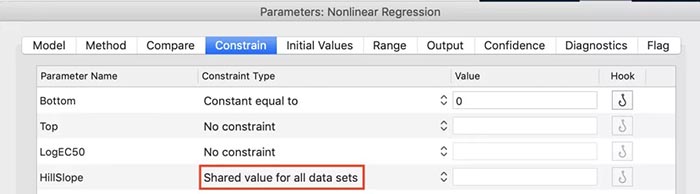
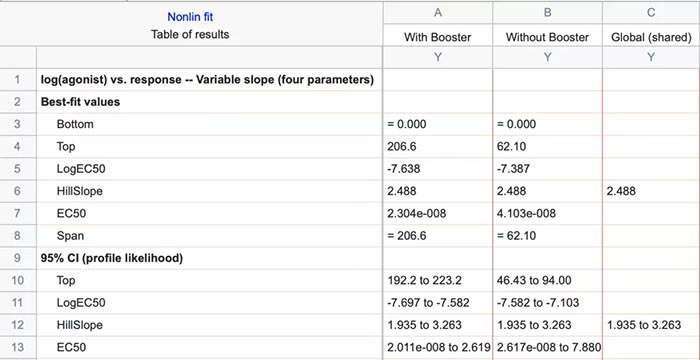
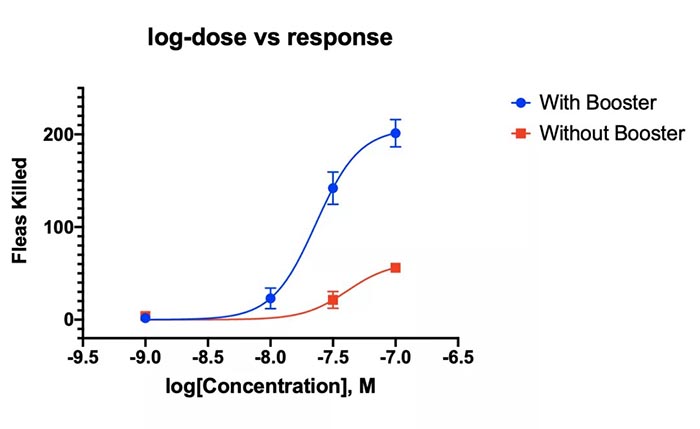
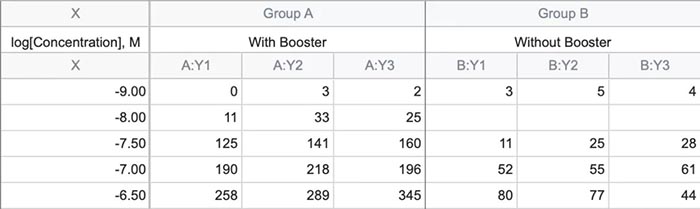
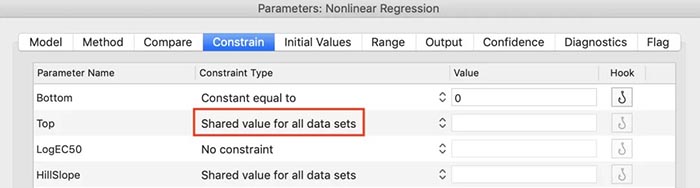
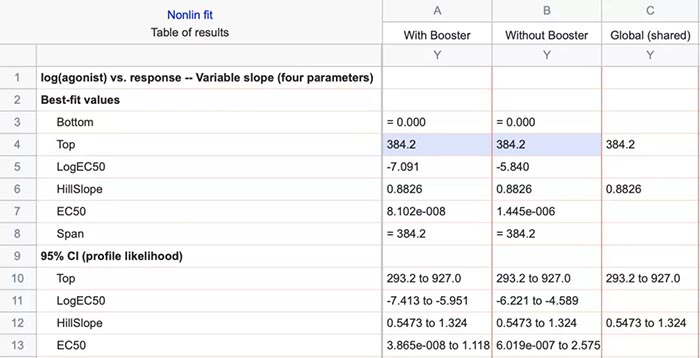
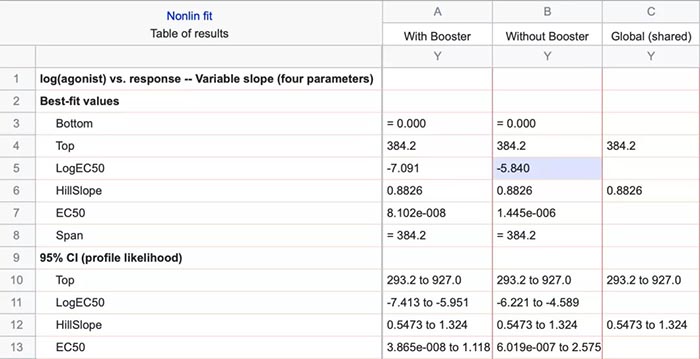
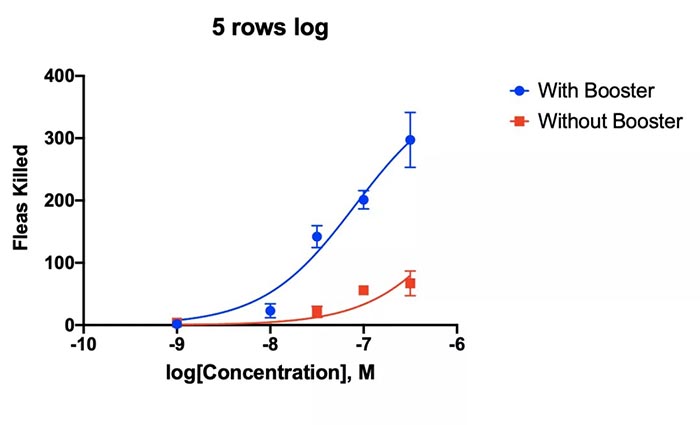
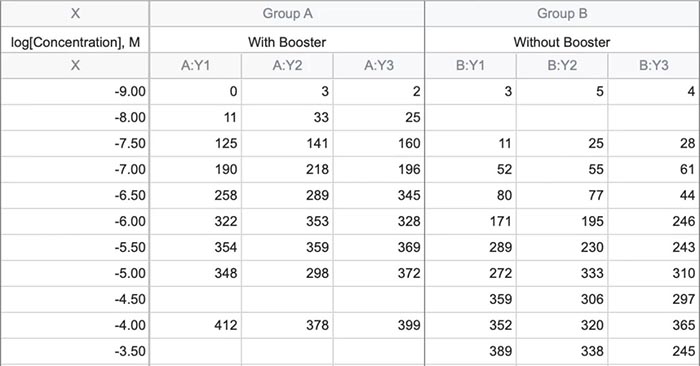
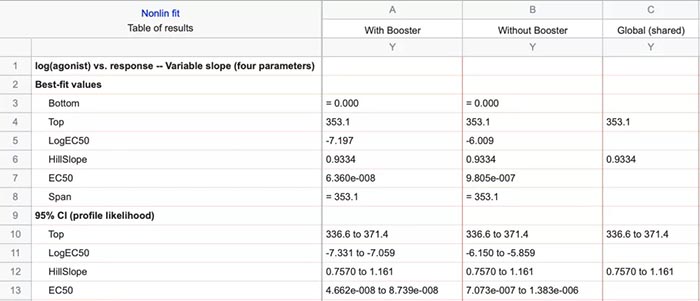
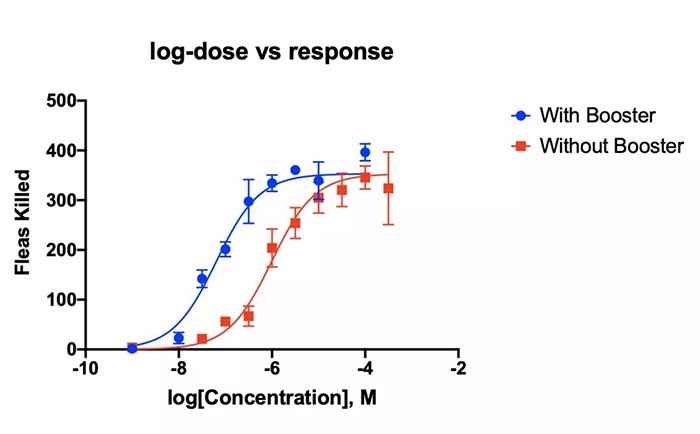
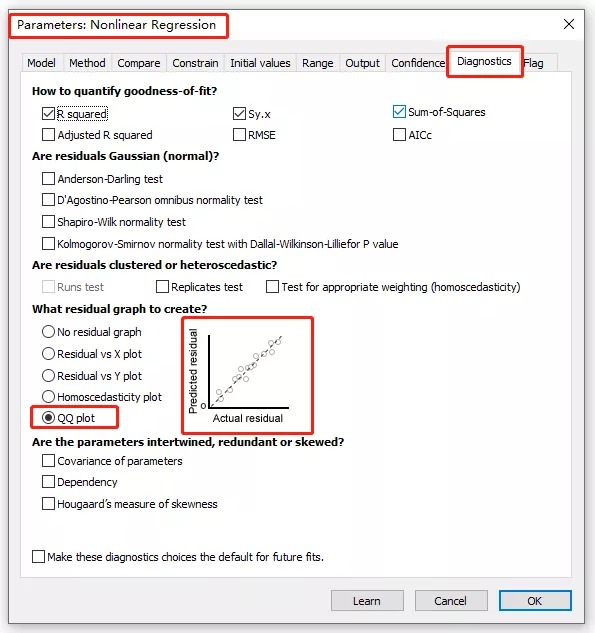
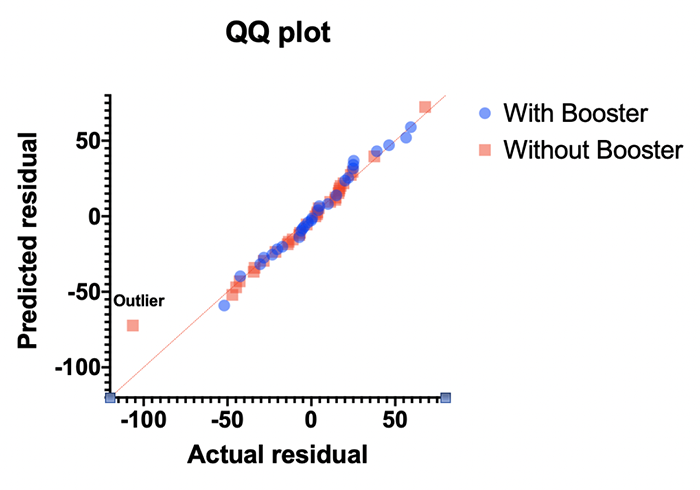
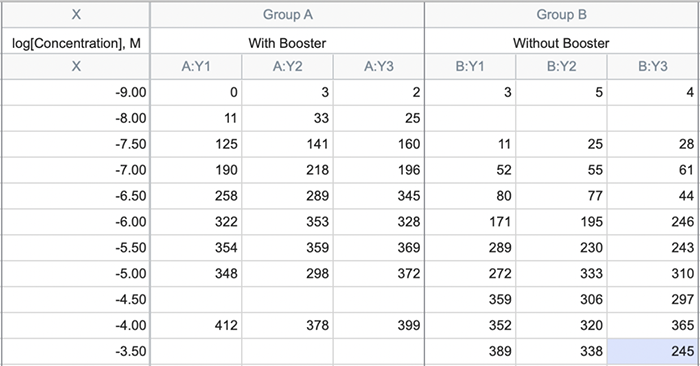
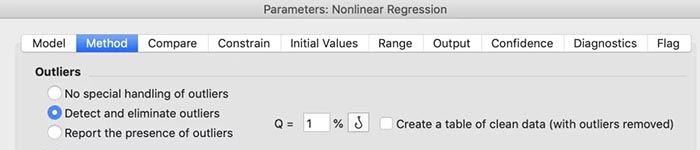
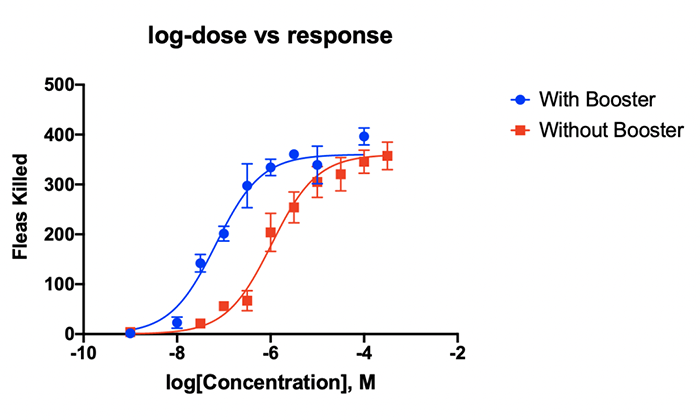
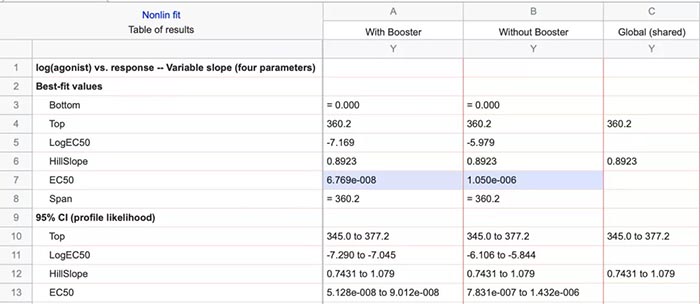
课题: 剂量反应案例研究:四参数Logistic 模型(4PL) 研究目标: 确定并对比有无增强剂条件下的EC50值 关键词: Graphpad Prism 统计分析 数据分析 医学作图 绘图软件 在试验开始之前,我们先来看看什么是四参数 Logistic 模型(4PL)。 1)一种是浓度 X 已经用以 10 为底的对数做了变换; 该模型中的四个参数包括:Top, Bottom, Hill Slope, EC50。 Top 是指最大响应。 在这项试验中,研究者认为高浓度时约为 400。这相当于杀死的 80% 的跳蚤。 Bottom 是指基线响应。 在浓度为零的情况下,研究者预测被杀死的跳蚤约为 0。 Hill Slope 是指曲线的坡度。 大于 1 的值表示呈陡坡,小于1的值表示呈缓坡。某些时候,它被设置为 1。 EC50 是指 Top 和 Bottom 之间引起反应的剂量。如果增强剂有效,「有增强剂」的 EC50 浓度应低于「无增强剂」的 EC50 浓度。 本试验中,Logistic 剂量反应模型的四个参数如下: 表1 Logistic 剂量反应模型的四个参数 图1 常规图 在对常规模型了解之后,我们使用实际的数据集来拟合此模型。 研究者进行一项小型试验,在四种浓度下各重复测量三次。在试验过程中,他们计算在500只跳蚤中被杀死的跳蚤数量。对于“无增强剂”组的数据,第二浓度组的数据被破坏了,所以如下方图2我们只得到三行数据。 图2 新建数据表 图3 数据表-输入数据 通过该试验数据绘制出的图4显示,随着剂量增加,反应也会增加。因此采用刺激模型比抑制模型更为合适。 图4 自动生成的图表 因为实际的浓度非常小,取对数可以让我们在一个更合理的范围上计算浓度。转换这些X值不会改变参数的最佳拟合值或它们的标准误差或置信区间。 图5 将浓度转换为对数显示 图6 数据表-对数转换结果 图7 四对数数据表的图表显示 我们可以从该初始数据集进行分析,操作如下: 【Analyze > XY analyses > Nonlinear regression (curve fit) > Dose-response -Stimulation > log (agonist) vs. response -- Variable slope (four parameters)】 【分析> XY 分析>非线性回归(曲线拟合)>剂量反应-刺激>对数(激动剂)与反应-可变斜率(四个参数)】 图8 Analyze操作步骤 在结果表(图9)中,可以看到“有增强剂”模型有一组完整的参数估计和置信区间,但另一边“无增强剂”模型被标记为“不明确的”,这表示其显示的数据结果是不可信的。 图9 结果页 自8.2版本起,Prism可以查看是哪些参数会导致不明确的拟合。这些被称为不稳定参数,可以在分析时通过从置信度选项卡(Confidence tab)中选择“识别不稳定参数(Identify unstable parameters)”来设置; 或者在工具栏的Analyze右侧的按钮(上图按钮↑)来修改参数。 图10 设置“识别不稳定参数” 可以看到在“无增强剂”模型中,Top参数是不稳定的(如图11结果页)。在这个模型中存在一个不稳定参数并不奇怪,因为四参数logistic模型需要4个或更多X浓度数据,而“无增强剂”数据集中只有3个浓度的值。 图11 结果页-分析结果更新 当我们遇到不明确的模型时,可以试着通过将一个或多个参数设置为常数(constant)来减少模型中的参数数量。这需要我们了解反应(response)的行为方式。在这个试验中,研究者相信在非常低的浓度下其反应应该是零,目前的数据也证实了这一点,所以我们将通过输入0作为Bottom参数的约束来减少每个模型的参数数量,从4个减少到3个。这将两个模型的参数总数从8个减少到6个。一般来说,你估计的参数越少,模型收敛(converge)的可能性就越大。具体操作如下: Analyze > XY analyses > Nonlinear regression (curve fit) > Dose-response -Stimulation > log (agonist) vs. response -- Variable slope (four parameters) 【分析> XY分析>非线性回归(曲线拟合)>剂量反应-刺激>对数(激动剂)与反应-可变斜率(四个参数)】 图12 设置Bottom参数约束 如下图13,将Bottom设置为0,但 “无增强剂”模型中仍然有不稳定的参数。 图13 结果页分析结果更新 再次减少需要估算的参数数量。研究者认为这两种模型应该具有相同的曲线坡度(Hill Slope)。通过共享坡度(Hill Slope)参数,参数数量将从6个减少到5个。操作如下, Analyze > XY analyses > Nonlinear regression (curve fit) > Dose-response -Stimulation > log (agonist) vs. response -- Variable slope (four parameters) 【分析> XY分析>非线性回归(曲线拟合)>剂量反应-刺激>对数(激动剂)与反应-可变斜率(四个参数)】 图14 设置Hill Slope参数的约束 这样一来两个模型都收敛了,可以看到对于所有参数我们都有相应的估计和置信区间(如图15)。 图15 结果页分析结果更新 研究者希望这两条曲线的Maximal response都在400左右,而这些模型的曲线图都没有呈现出接近这个值的趋势。 图16 图表 为了更好地估计Top参数,研究者决定在-6.5的对数浓度(log concentration)下收集更多的数据(见图17),并确保它们具有相同的maximal response。通过Prism 8中的约束选项卡(the Constrain tab)来共享Top参数,只保留LogEC50参数不受约束(见图18)。操作如下: 【Analyze > XY analyses > Nonlinear regression (curve fit) > Dose-response -Stimulation > log (agonist) vs. response -- Variable slope (four parameters)】 【分析> XY分析>非线性回归(曲线拟合)>剂量反应-刺激>对数(激动剂)与反应-可变斜率(四个参数)】 图17 五数据表更新 图18 设置Top参数约束 这个改进不错,两组模型中的Top参数都接近400了(如图19)。 图19 结果页分析结果更新 – Top 但可能会担心“无增强剂”模型中EC50值的估计,可以看到该模型中对数值是-5.84(如下图20)。 图20 结果页分析结果更新 – LogEC50 下面图21是最新生成的图表,在对数刻度上没有任何-5.84的数据,是因为我们对EC50的估计是基于外推法,意味着我们是在数据范围之外做预测。 图21 图表 为了避免这种外推(extrapolation),研究者决定收集额外的数据来捕捉“无增强剂”的剂量反应曲线的中间和右侧。 图22 数据表更新 在收集这些数据之后,没有通过外推法去估计,而是如更窄的置信区间所示,我们很好地估计了各项参数。 图23 结果页分析结果更新 如下图(图24)所示,我们按预期拟合了数据。 图24 图表 但是整个分析到这里还没有结束。由于到目前为止我们所看到的图显示的是均值而非原始数据,因此查看残差图以检查异常值是非常重要的。下方的QQ residual plot图(QQ残差图)(图26)显示存在一个异常值(outlier)。 图25 设置显示“QQ Plot” 图26 残差图 将这个异常值映射回数据集,可以看到它是在“无增强剂”组的高剂量情况下发生的(如下图27)。这个值输入错误,应为345。 图27 数据表更新 注意,这一点也可以通过在Method选项卡中选择“检测和消除异常值(Detect and eliminate outliers)”来识别和删除。操作如下, Analyze > XY analyses > Nonlinear regression (curve fit) > Dose-response -Stimulation > log (agonist) vs. response -- Variable slope (four parameters) 【分析> XY分析>非线性回归(曲线拟合)>剂量反应-刺激>对数(激动剂)与反应-可变斜率(四个参数)】 图28 设置监测和消除异常值 图29 结果表-异常值提示 进行更改后,可以看到最终图形显示出更好的拟合度。 图30 最终图表 最终结果表的Bottom设置为0,两个模型的Top估计为360.2、Hill Slope估计为0.8923,“有增强剂”的EC50为6.769 * 10的负8次方,“无增强剂”的EC50为1.05 * 10的负6次方。根据这两个EC50值的比值,“无增强剂”浓度需要比“有增强剂”浓度大15.5倍,才能获得与“有增强剂”相同的效果。 图31 结果表最终分析结果 总结 回顾本篇案例研究,我们讨论了包括以下几个方面: 4PL模型参数的含义; 如何检查不明确模型和不稳定参数; 如何将参数设置为常数及其带来的好处; 如何跨数据集共享参数及其带来的好处; 如何避免外推; 如何检查异常值
四参数 Logistic 方程有如下两种形式:
Model
Y=Bottom+(Top-Bottom)/(1+10^((LogEC50-X)*HillSlope))
2)一种是 X 没有变换过。对于任何一种方式,Prism 中的参数估计值、标准误和置信区间都是相同的;
Model
Y=Bottom + (X^Hillslope)*(Top-Bottom)/(X^HillSlope + EC50^HillSlope)




相关推荐:
「视频教程」GraphPad Prism 8 软件操作教程 中文字幕
「视频教程」手把手教你用GraphPad Prism做符合SCI投稿的标准图
GraphPad Prism 7 for Win / Mac 完美破解版 统计绘图软件 附安装教程
GraphPad Prism 8.4.3 for Win/Mac 最新完美激活中英文版医学绘图软件+安装教程
GraphPad Prism 9 for Win/Mac 完美学习版+安装教程














